켈빈 함수의 개요
켈빈 함수(Kelvin function)는 수학과 물리학에서 매우 중요한 특수함수로, 실제 세계의 물리 현상, 즉 자연의 파동과 에너지 흐름을 이해하고 정확하게 기술하기 위해 만들어진 정교한 수학적 표현체계입니다. 주로 복소수 영역의 베셀 함수(Bessel function)를 실수 인수(real argument)에 대해 다루기 쉽게 만든 덕분에, 전자기학, 열역학, 음향학 등에서 매우 실용적인 역할을 합니다.
이 함수는 특히 전자기학, 열전달, 진동, 음향 등 여러 공학 분야에서 필수적으로 등장합니다. 켈빈 함수는 간단히 말해 복소 베셀 함수를 실수부와 허수부로 나누어 표현한 것으로, 실수 범위에서 계산이 가능하도록 만든 함수입니다. 이런 이유로 복잡한 복소수 계산을 직접 다루지 않고도 실제 물리현상을 표현할 수 있게 해줍니다. 켈빈 함수의 개념은 윌리엄 톰슨 경, 즉 켈빈 경(Lord Kelvin)의 이름을 따서 명명되었습니다.
정의와 수학적 배경
켈빈 함수는 베셀 함수 Jν(z)J_ν(z)Jν(z)에서 유도됩니다. 일반적인 베셀 함수는 복소수 인수 zzz를 갖는 함수이지만, 켈빈 함수는 그 인수가 실수 xxx일 때 계산이 용이하도록 정의된 것입니다. 0차 베셀 함수 J0(z)J_0(z)J0(z)를 기준으로 정의할 때, 켈빈 함수는 다음과 같이 주어집니다.
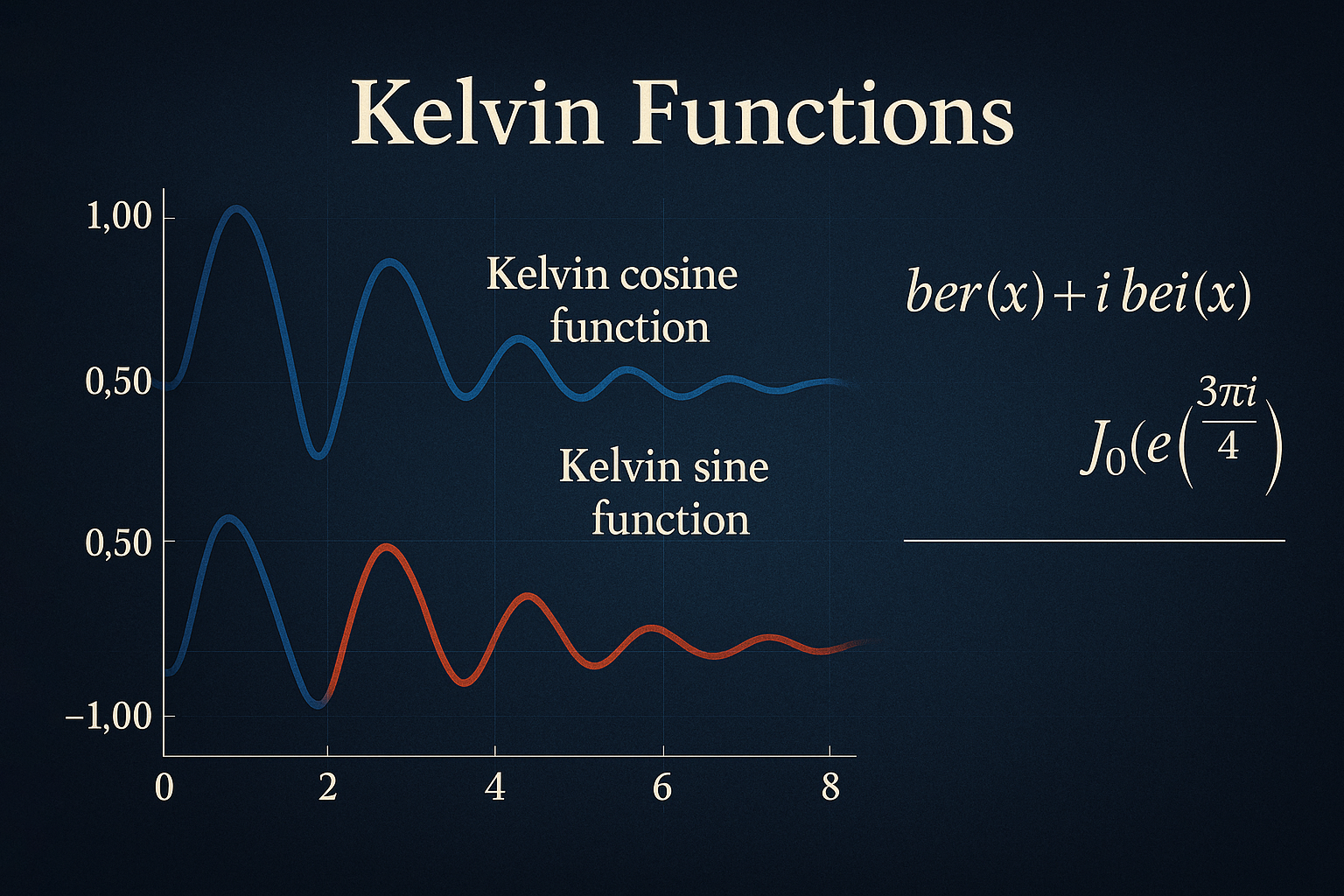
ber(x)+i bei(x)=J0(xe3πi/4)\text{ber}(x) + i\,\text{bei}(x) = J_0(x e^{3πi/4})ber(x)+ibei(x)=J0(xe3πi/4)
여기서 ber(x)\text{ber}(x)ber(x)는 Kelvin cosine function, bei(x)\text{bei}(x)bei(x)는 Kelvin sine function이라 부릅니다. 다시 말해, ber(x)는 복소 베셀 함수의 실수부이고, bei(x)는 허수부입니다. 이 정의를 통해 켈빈 함수는 실수 영역에서의 진동성과 감쇠 특성을 동시에 표현할 수 있습니다.
ber(x)와 bei(x)의 성질
ber(x)와 bei(x)는 각각 다른 물리적 의미를 가지지만, 서로 밀접하게 연결되어 있습니다. ber(x)는 코사인(cosine) 형태의 변화를 따르며, bei(x)는 사인(sine) 형태의 변화를 보입니다. 두 함수 모두 진동성을 가지지만, 일반적인 삼각함수와는 달리 진폭이 일정하지 않고 점점 감쇠하는 형태를 띱니다. 이는 복소수의 위상 변화에 따라 발생하는 진폭 감소 효과를 반영한 결과입니다.
작은 xxx 값에 대해서는 ber(x)와 bei(x)가 다음과 같이 급수 전개로 근사될 수 있습니다.
ber(x)=1−(x4)22(2!)2+(x8)24(4!)2−⋯\text{ber}(x) = 1 - \frac{(x^4)}{2^2 (2!)^2} + \frac{(x^8)}{2^4 (4!)^2} - \cdotsber(x)=1−22(2!)2(x4)+24(4!)2(x8)−⋯ bei(x)=(x2)21(1!)2−(x6)23(3!)2+(x10)25(5!)2−⋯\text{bei}(x) = \frac{(x^2)}{2^1 (1!)^2} - \frac{(x^6)}{2^3 (3!)^2} + \frac{(x^{10})}{2^5 (5!)^2} - \cdotsbei(x)=21(1!)2(x2)−23(3!)2(x6)+25(5!)2(x10)−⋯
이 급수 전개는 작은 입력 값에서 ber(x)와 bei(x)가 매우 완만하게 변화함을 보여줍니다. 반대로 xxx가 커질수록 두 함수는 진폭이 서서히 증가하면서 점점 복잡한 진동 형태를 나타냅니다.
물리학적 의미와 응용
켈빈 함수는 단순히 수학적 호기심으로 정의된 함수가 아닙니다. 실제로 이 함수는 여러 공학 문제에서 중심적인 역할을 합니다. 대표적인 예가 스킨 효과(skin effect) 입니다. 스킨 효과는 교류 전류가 도체의 표면 근처를 따라 흐르고, 중심부로 갈수록 전류 밀도가 급격히 줄어드는 현상입니다. 이 현상은 고주파 전류가 흐를 때 특히 두드러지며, 도체의 내부 자기장과 전류 밀도를 계산할 때 켈빈 함수가 필수적으로 사용됩니다.
전도체 내부에서의 전류 밀도 분포를 표현하는 식은 종종 ber(x)와 bei(x)를 포함합니다. ber(x)는 전류의 실수 성분을, bei(x)는 위상이 90도 차이나는 허수 성분을 나타냅니다. 이 두 함수를 결합하면 전류의 전체 위상 및 진폭 변화를 정확히 계산할 수 있습니다.
또한 켈빈 함수는 열전도 문제, 복합 매질 내의 전자파 전파, 진동판의 표면 응력 해석 등에서도 등장합니다. 특히 원형 대칭을 가진 문제에서 베셀 함수가 기본적으로 사용되기 때문에, 켈빈 함수는 이러한 상황에서 실수 해석을 가능하게 하는 도구로 널리 쓰입니다.
복소수 표현과 위상 해석
켈빈 함수의 가장 흥미로운 점 중 하나는 복소수 평면에서의 기하학적 의미입니다. ber(x)와 bei(x)는 복소수 평면에서 서로 직교하는 성분으로, 하나의 복소수 함수로 묶으면 나선형 경로를 그립니다. 이는 진폭이 점점 커지는 감쇠형 나선으로 시각화할 수 있으며, 전자기파의 위상 변화나 진동 시스템의 감쇠 모드와 밀접하게 연관됩니다.
복소 함수의 관점에서 보면, 켈빈 함수는 단순히 실수부와 허수부를 분리한 것이 아니라, 복소수 위상 회전을 실수 축으로 투영한 결과입니다. 이런 이유로 켈빈 함수는 주파수 응답 해석이나 복소 임피던스 해석에서 매우 유용하게 쓰입니다.
계산 방법과 수치적 접근
켈빈 함수는 단순한 닫힌 형태의 해를 가지지 않기 때문에, 대부분의 경우 수치적 계산을 통해 값을 구합니다. 수학 소프트웨어(예: MATLAB, Mathematica, SciPy 등)에서는 ber(x), bei(x), ker(x), kei(x) 등 네 가지 켈빈 함수를 기본 내장함수로 제공합니다. 여기서 ker(x)와 kei(x)는 감쇠형 켈빈 함수로, 수정 베셀 함수(modified Bessel function)에 기반한 형태입니다. 이들은 열전도나 복사 감쇠와 관련된 문제에서 자주 등장합니다.
수치 계산 시에는 고정밀 급수 전개, 아심프토틱(점근) 근사, 또는 보간법을 사용합니다. 예를 들어, 큰 x 값에서는 켈빈 함수가 진동하면서 감쇠하기 때문에, 단순한 급수 전개로는 계산이 어렵습니다. 따라서 고차 항을 포함한 근사식이나, 이미 계산된 표를 기반으로 한 보간 기법을 사용합니다.
역사적 배경과 명명 이유
켈빈 함수의 명칭은 19세기 물리학자 윌리엄 톰슨 경, 즉 켈빈 경(Lord Kelvin) 의 이름에서 유래되었습니다. 그는 열역학 제2법칙의 정립과 절대온도 단위(Kelvin scale) 제정으로 유명하지만, 동시에 복잡한 전자기 문제의 해석에도 깊은 공헌을 했습니다. 켈빈 함수는 그가 전자기 진동과 전류 분포를 연구하는 과정에서 처음 제안한 형태 중 하나로, 이후 수학자들이 이를 일반화하고 체계화하면서 현재의 정의에 이르게 되었습니다.
수학적 확장과 관련 함수
켈빈 함수는 베셀 함수뿐 아니라, 다른 특수함수와도 깊은 관련이 있습니다. 예를 들어, 수정 베셀 함수 Iν(z)I_ν(z)Iν(z)와 Kν(z)K_ν(z)Kν(z)는 열전달 문제에서 자주 등장하며, 이들의 실수부와 허수부를 분리하면 ker(x)와 kei(x)라는 감쇠형 켈빈 함수가 만들어집니다.
이 네 가지 함수 — ber(x), bei(x), ker(x), kei(x) — 는 각각 진동형과 감쇠형의 두 쌍을 이루며, 서로 상보적인 역할을 합니다. ber와 bei는 진동하며 에너지 전달을 나타내고, ker와 kei는 감쇠를 나타내어 에너지 손실이나 열 확산과 같은 현상을 표현합니다.